Data Analyst

Statistical Thinking

Well Known distributions

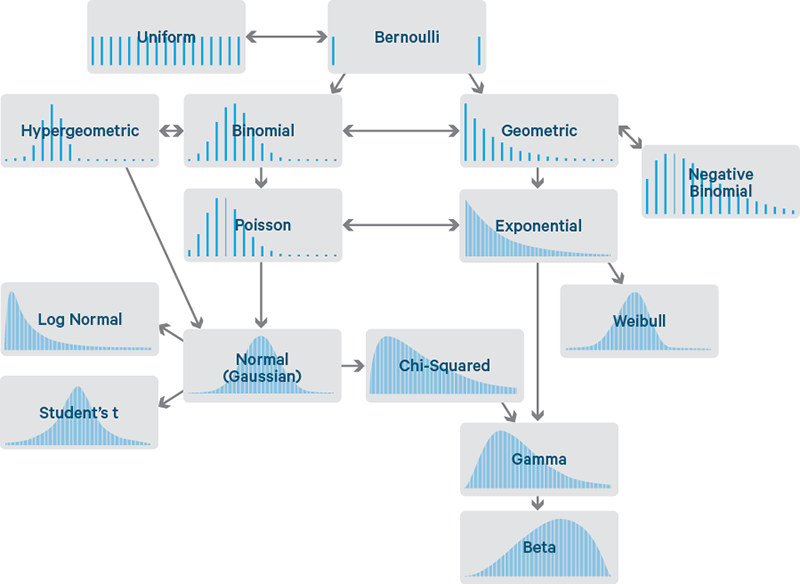
Why Probability Distributions?

A probability distribution is a mathematical description of how values occur.

In retail analytics they help us answer questions like:

• How long until the next customer arrives?
  
• How many customers enter per hour?
  
• What is the chance a customer buys after viewing a product?
  
• What happens when we know only a range but nothing else?

Normal Distribution

These first five people have heights around the high 144 to high 200.

[174, 169, 175, 182, 168]

Histogram with 5 People

Wider Bins

Narrower Bins

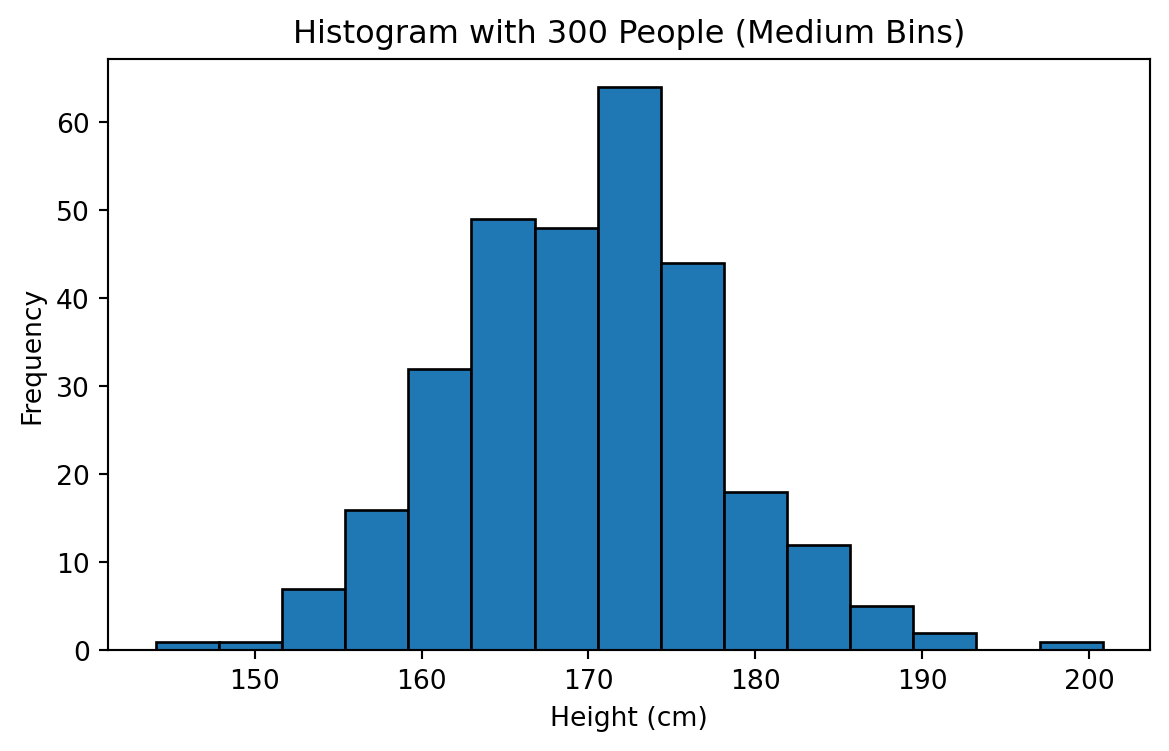
Increasing Sample Size to 300

Generalization

\[ f(x) = \frac{1}{\sigma \sqrt{2\pi}} \exp\left( -\,\frac{(x - \mu)^2}{2\sigma^2} \right) \]

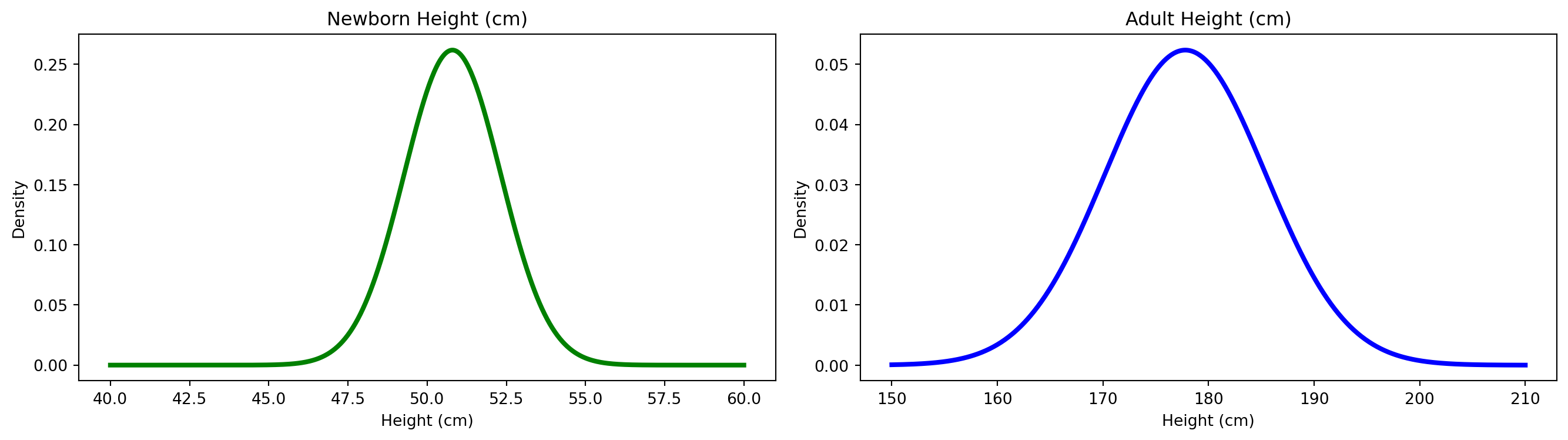
Two Normal Distributions

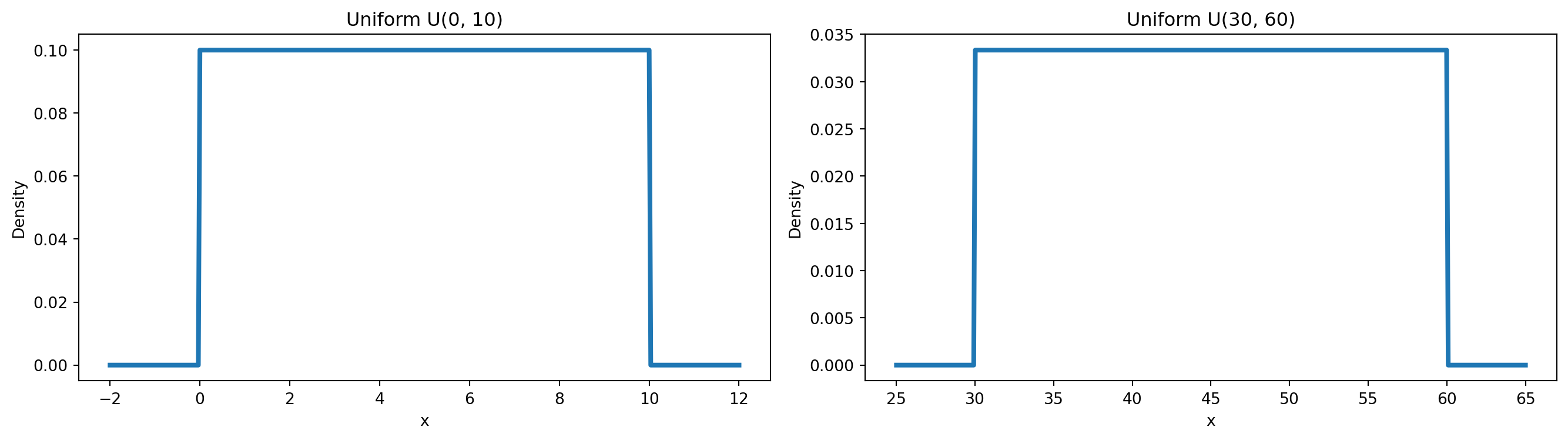
Uniform

• Random checkout routing delay (e.g., anywhere between 0–10 seconds)
• Random discount reveal time in a promotion mini-game
• Random product display duration on a marketing banner
• Random delivery pickup window (e.g., 14:00–16:00)
• Simulation of uncertain but bounded retail processes
• Any situation where the value is known to be in a range, and all outcomes inside that range are equally likely

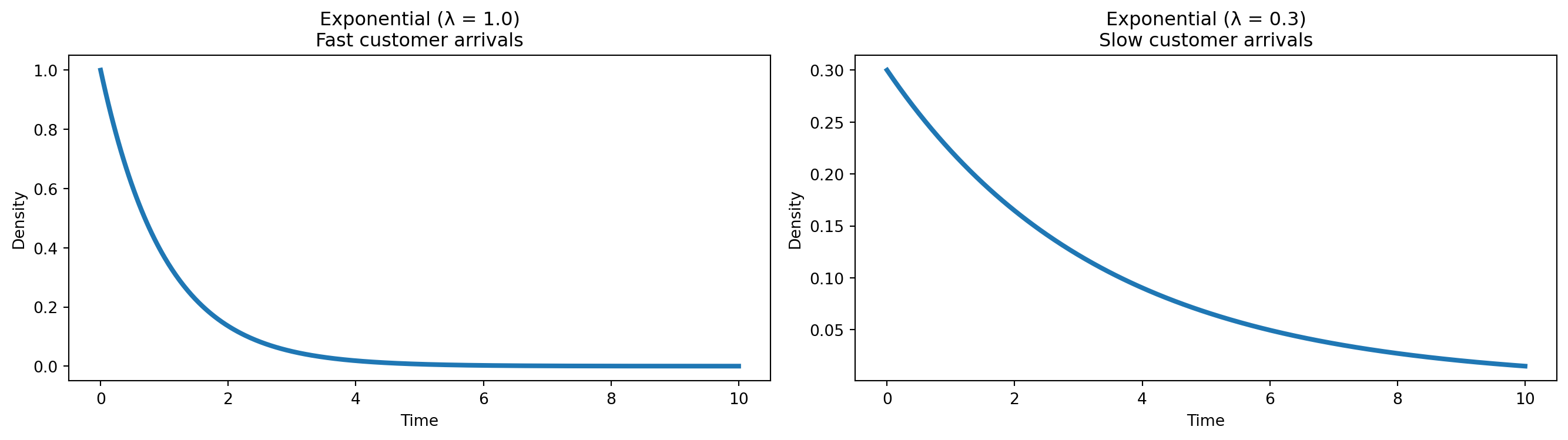
Exponential

• Time between customers arriving at checkout
  
• Time between online purchases
  
• Time until next product scan at self-checkout
  
• Time between clicks in an online session
  
• Time until next customer picks up a product from the shelf
  
• Any situation involving “waiting time until the next event” in retail

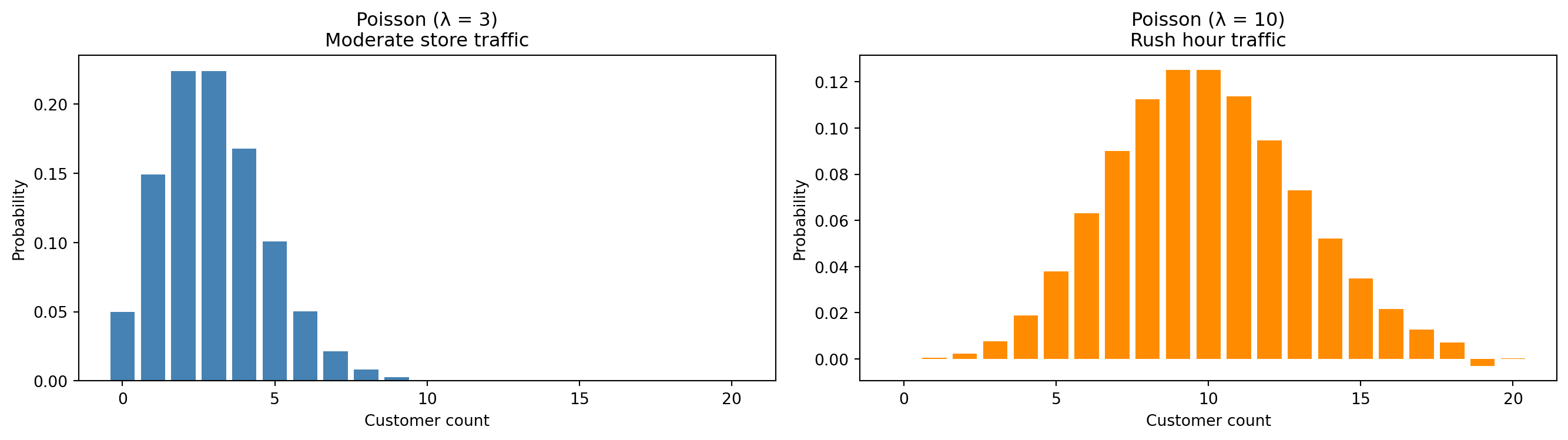
POISSON

Poisson

• Number of customers entering per hour
  
• Number of online orders per minute
  
• Number of carts abandoned in each 10-minute window
  
• Number of returns processed per 30-minute interval
  
• Number of loyalty signups per hour
  
• Any situation involving “how many events occur in a fixed time window”

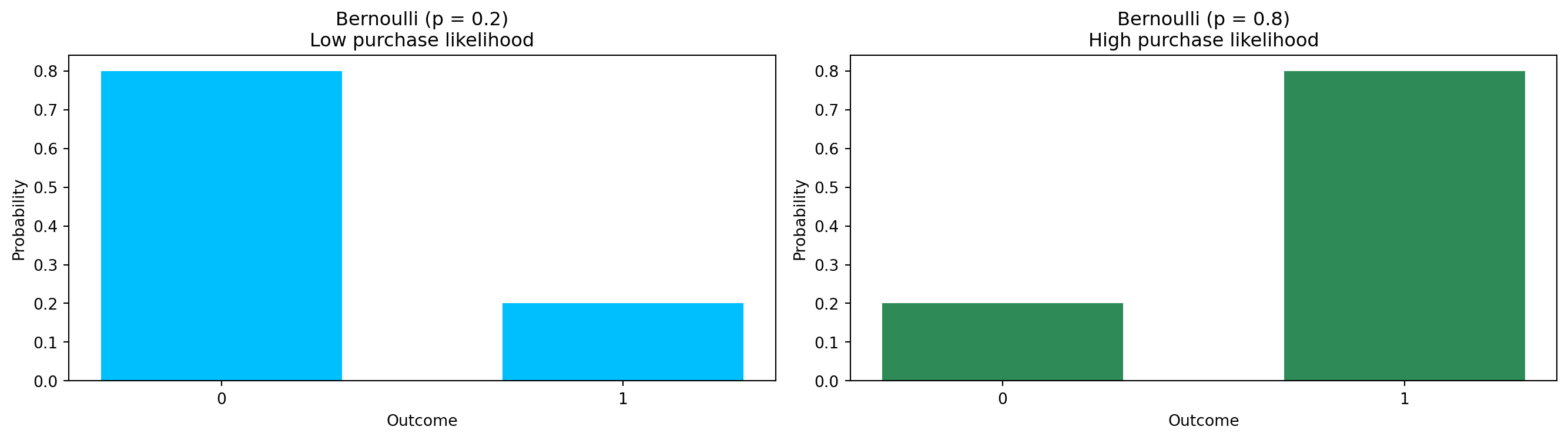
Bernoulli

• Customer buys (1) or does not buy (0)
  
• Customer clicks a product (1) or ignores it (0)
  
• Customer redeems a coupon (1) or not (0)
  
• Loyalty signup (1) or no signup (0)
  
• Email open vs. no open
  
• Any situation involving a single yes/no retail event

Comparison of Distributions

Comparison | 1

Uniform:

• All values inside a range equally likely
  
• Random checkout delay
  
• Random promotion reveal time
  
• Random banner display duration
  
• Random delivery pickup window

Exponential:

• Waiting time until next event
  
• Time between customer arrivals
  
• Time between online purchases
  
• Time between product scans at self-checkout

Comparison |2

Poisson:

• Number of events in a fixed interval
  
• Customers entering per hour
  
• Online orders per minute
  
• Carts abandoned per 10-minute window
  
• Returns processed per interval

Bernoulli:

• Single yes/no outcome
  
• Buy (1) vs. no-buy (0)
  
• Click vs. no-click
  
• Coupon redeemed vs. not redeemed
  
• Loyalty signup vs. no signup

CLT

Why its important

The CLT allows analysts to:

• Estimate true average revenue per customer
  
• Compare stores or campaigns reliably
  
• Decide whether a promotion increased average spend
  
• Build confidence intervals for KPIs
  
• Run A/B tests using sample means
  
• Make strong conclusions from limited data